Числа на числовой прямой

Презентация по математике преподавателя « Орского технического техникума имени А. И. Стеценко » филиал пос. Энергетик Николаевой Натальи Юрьевны. Оренбургская область Новоорский район посёлок Энергетик.

Числа

«Мысль выражать все числа девятью знаками, придавая им, кроме значения по форме, еще и значение по месту, настолько проста, что именно из-за этой простоты трудно понять, насколько она удивительна».

Пьер Симон Лаплас (1749-1827)

•   N - натуральные числа

•   Z - целые числа

•   Q - рациональные числа

• R -действительные числа

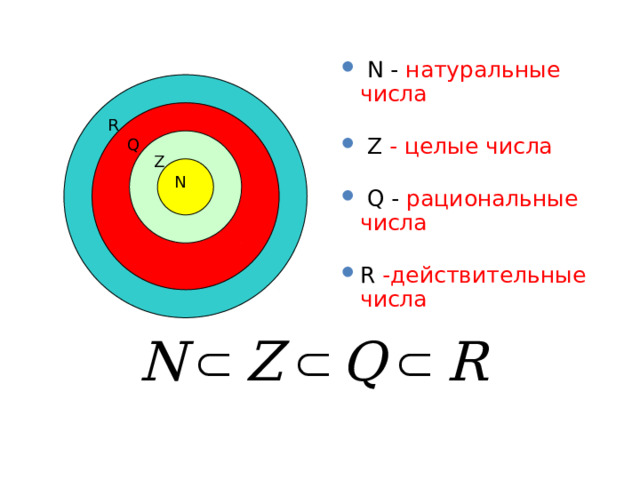
R

Q

Z

N

Н атуральные числа  

Числа 1, 2, 3, …, употребляемые при счете предметов, образуют множество натуральных чисел .

Обозначают буквой N.

Например, запись 27Є N читается: «27 принадлежит множеству натуральных чисел».

Любое натуральное число в десятичной системе счисления записывается с помощью цифр 0, 1 ,2 ,3 ,4 ,5 ,6 ,7 ,8 ,9.

Например, запись 2457 означает, что 2457=2•1000+4•100+5•10+7.

Вообще если а - цифра тысяч, b –цифра сотен, d- цифра десятков и c- цифра единиц то имеем а • 1000+b•100+ c •10+d .

Используется также сокращенная запись аbcd.

1 2 3 4 5

Целые числа

Натуральные числа, противоположные им числа и число нуль Составляют множество целых чисел.

Обозначают буквой Z.

Например, запись -27Є Z читается: «-27 принадлежит множеству целых чисел».

-5 -4 -3 -2 -1 0 1 2 3 4 5

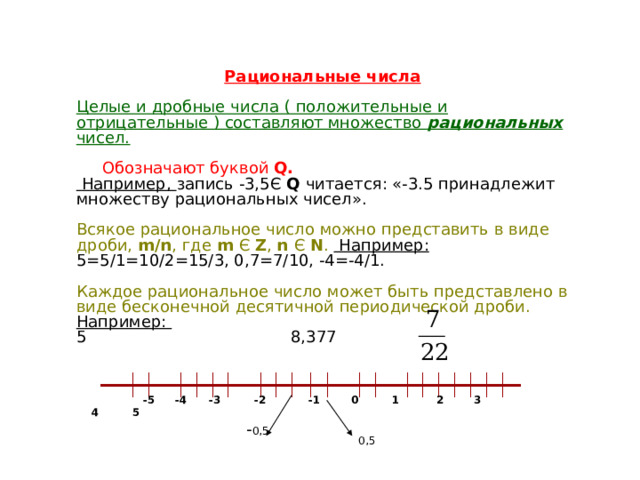
Рациональные числа

Целые и дробные числа ( положительные и отрицательные ) составляют множество рациональных чисел.

Обозначают буквой Q.

Например, запись -3,5Є Q читается: «-3.5 принадлежит множеству рациональных чисел».

Всякое рациональное число можно представить в виде дроби, m/n , где m Є Z , n Є N . Например: 5=5/1=10/2=15/3, 0,7=7/10, -4=-4/1.

Каждое рациональное число может быть представлено в виде бесконечной десятичной периодической дроби. Например:

5 8,377

-5 -4 -3 -2 -1 0 1 2 3 4 5

- 0,5

0,5

5=5,000000….=5,(0)

8,377=8,377…=8,3(7)

Каждое рациональное число может быть представлено в виде конечной десятичной дроби или бесконечной десятичной периодической дроби.

Рациональное число (лат. ratio — отношение, деление, дробь) — число, представляемое обыкновенной дробью , где числитель m — целое число, а знаменатель n — натуральное число. Такую дробь следует понимать как результат деления m на n, даже если нацело разделить не удаётся. В реальной жизни рациональные числа используются для счёта частей некоторых целых, но делимых объектов, например, тортов или других продуктов, разрезаемых на несколько частей

Множество рациональных чисел

Множество рациональных чисел обозначается и может быть записано в виде:

Нужно понимать, что численно равные дроби

такие как, например, и , входят в это множество как

одно число. Поскольку делением числителя и знаменателя дроби на их наибольший общий делитель можно получить единственное несократимое представление рационального числа, то можно говорить об их множестве как о множестве несократимых дробей со взаимно простыми целым числителем и натуральным знаменателем:

Рациональные числа как бесконечные десятичные дроби

Для всех рациональных чисел можно использовать один и тот же способ записи. Рассмотрим

1. Целое число 5

5,000

2. Обыкновенную дробь

0, 3(18)

3. Десятичную дробь 8,377

8,3(7)

Пример. Записать в виде обыкновенной дроби бесконечную десятичную периодическую дробь.

Положим, что х=1,(23), т.е. 1,232323…

100х=123,2323…

100х=123,2323…

• х=1,2323…

99х=122

х=

Итак: 1,(23)=

Положим х=1,5(23)=1,52323…

Сначала умножим на 10.

Получим 15,2323.., а потом ещё на 100

1000х=1523,2323…

• 10х= 15,232323…

990х=1508

х=

Итак: 1,5(23)=

Пусть х=0,1(9), тогда

100х=19,999…

-10х= 1,999…

90х=18

Итак, х=0,1(9)= = , но

= 0,2

Замечание: В примере мы видим, что 0,1(9)=0,2(0). Аналогично можно установить, что 2,45(9)=2,46(0) и т.д. Поэтому обычно десятичные дроби с периодом 9 не рассматриваются, заменяют их соответственно дробями с периодом 0.

Иррациональные числа

• К иррациональным числам относятся бесконечные десятичные непериодические дроби. Например: 3,01001…,
• π ≈ 3,145926…,

√ 2 ≈ 1,4…

√ 3

≈ 1,7

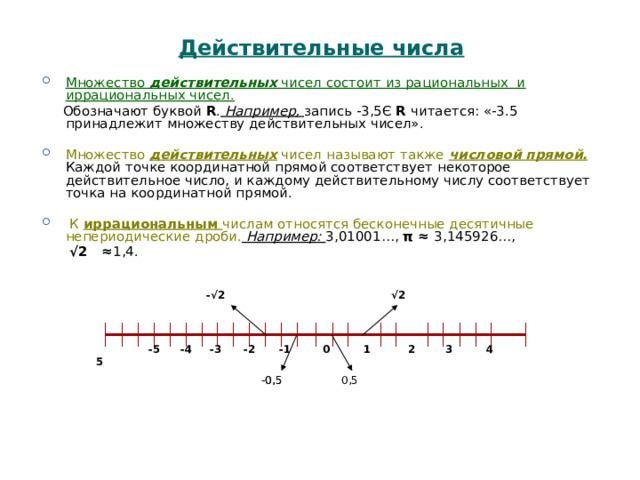
Действительные числа

• Множество действительных чисел состоит из рациональных и иррациональных чисел.

Обозначают буквой R . Например, запись -3,5Є R читается: «-3.5 принадлежит множеству действительных чисел».

• Множество действительных чисел называют также числовой прямой. Каждой точке координатной прямой соответствует некоторое действительное число, и каждому действительному числу соответствует точка на координатной прямой.

• К иррациональным числам относятся бесконечные десятичные непериодические дроби. Например: 3,01001…, π ≈ 3,145926…,

√ 2 ≈ 1,4.

-√2

√ 2

-5 -4 -3 -2 -1 0 1 2 3 4 5

-0,5

-0,5

0,5

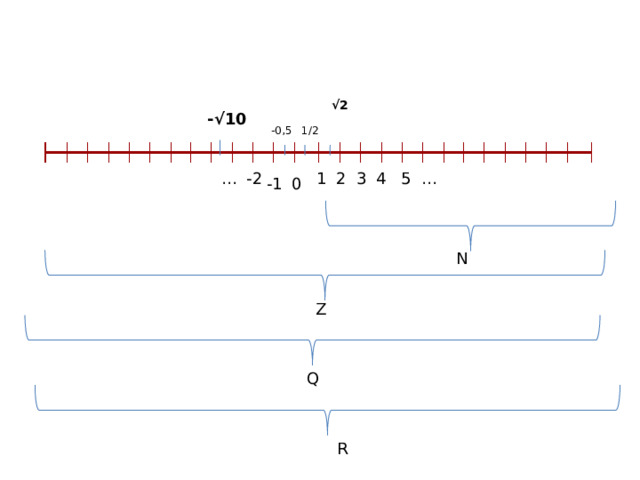
√ 2

-√10

1/2

-0,5

…

-2

…

5

4

3

2

1

0

-1

  N

Z

Q

R

Множества, операции над ними

«Множество есть многое, мыслимое нами как единое».

Основоположник теории множеств немецкий математик

Георг Кантор

(1845-1918)

Понятие множества принадлежит к числу основных, неопределяемых понятий математики. Множество – набор, совокупность, собрание каких-либо объектов (элементов), обладающих общим для всех их характеристическим свойством. Примеры множеств: множество учащихся в данной аудитории; множество людей, живущих на нашей планете в данный момент времени; множество точек данной геометрической фигуры; множество чётных чисел; множество корней уравнения х2-5х+6=0; множество действительных корней уравнения х2+9=0;

Объекты, составляющие данное множество, называют его элементами. Множество обычно обозначают большими латинскими буквами, а элементы множества − малыми латинскими буквам. Если элемент, а принадлежит множеству А, то пишут: а А Если а не принадлежит А, то пишут: а А.

В математике часто исследуются так называемые числовые множества, т.е. множества, элементами которых являются числа. Для самых основных числовых множеств утвердились следующие обозначения: N - множество всех натуральных чисел; Z - множество всех целых чисел; Q - множество всех рациональных чисел; R - множество всех действительных чисел. Приняты также обозначения Z+ , Q+, R+ соответственно для множеств всех неотрицательных целых, рациональных и действительных чисел, и Z¯, Q¯, R¯ -для множеств всех отрицательных целых, рациональных и действительных чисел.

Способы задания множества

• перечисление элементов множества;

А={a; b; c; …;d}

• указание характеристического свойства элементов множества, т.е. такого свойства, которым обладают все элементы данного множества и только они.

А={х | х2-5х+6=0}.

Поставьте вместо звездочки знак так, чтобы полу- чить правильное утверждение: 1) 5 * N; 2) –5 * Q; 3) 3,14 * Q; 4) 2 * R; 5) 0 * N; 6) − 12 * Z; 6) π * Q; 8) 3 * ∅

Задайте перечислением элементов множество: 1) A = { x | x N, x 2 – 1 = 0}; 2) B = { x | x Z, | x | C = { x | x N, x ≤ 15, x = 7 k , k Z}.

Действия над множествами

• Включение и равенство множеств

Пусть Х и У – два множества. Если каждый элемент х множества Х является элементом множества У, то говорят, что множество Х содержится во множестве У и пишут: Х У .

Говорят также, что Х включено в У или У или что Х является подмножеством множества У.

Если для двух множеств Х и У одновременно имеют место два включения т.е. Х есть подмножество множества У и У есть подмножество множества Х, то множества Х и У состоят из одних и тех же элементов. Такие множества Х и У называют равными и пишут: Х=У.

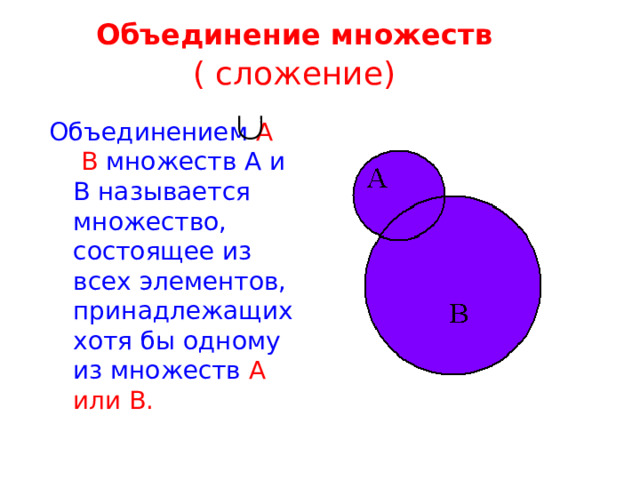
Объединение множеств ( сложение)

Объединением А В множеств А и В называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из множеств А или В.

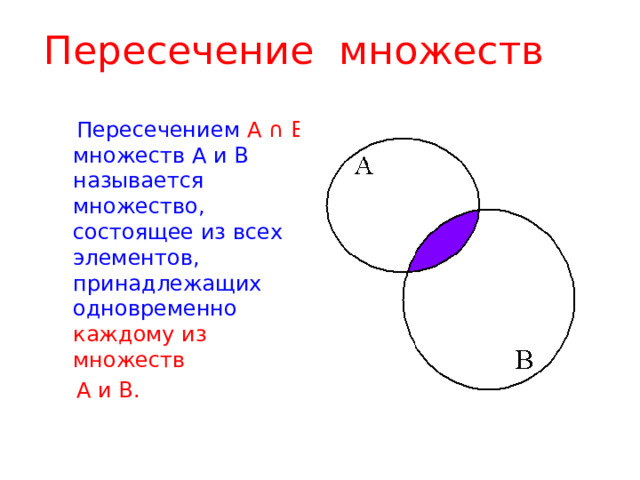
Пересечение множеств

Пересечением А ∩ В множеств А и В называется множество, состоящее из всех элементов, принадлежащих одновременно каждому из множеств

А и В.

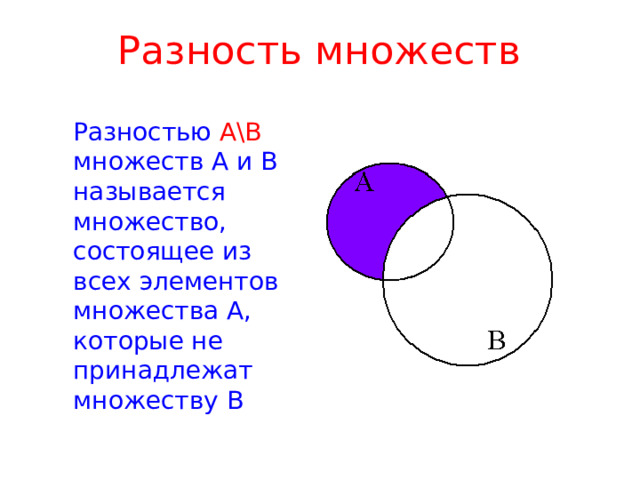
Разность множеств

Разностью А\В множеств А и В называется множество, состоящее из всех элементов множества А, которые не принадлежат множеству В