Тема: Барабарсыздыктар, касиеттери, барабарсыздыктарды далилдъъ.
Барабарсыздыктар.
Барабарсыздыктардын касиеттери.
Барабарсыздыктарды далилдъъ жолдору.
Барабарсыздыктар
Аныктама: Эки туюнтманын 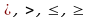 белгилери аркылуу бириктирилип жазылышы барабарсыздык деп аталат.
белгилери аркылуу бириктирилип жазылышы барабарсыздык деп аталат.
Мисалы: 5 ж.б.
ж.б.
Мында туура жана туура эмес барабарсыздыктар бар, жогорку келтирилген мисал-дарда биринчиси туура, ал эми экинчиси туура эмес барабарсыздык болуп эсептелет. Барабарсыздык деп ошондой эки туюнтманын  белгиси аркылуу бириктирилип жазылы-шын айтууга болот. Мисалы:
белгиси аркылуу бириктирилип жазылы-шын айтууга болот. Мисалы: 
Аныктама: Барабарсыздыктын аныкталуу областы же ъзгърмълърд\н кабыл алууга м\мк\н болгон маанилери деп ага катышкан ъзгърмълърд\н кабыл алууга м\мк\н болгон маанилери деп ага катышкан ъзгърмълърд\н, барабарсыздыктын эки жагы теё мааниге ээ боло турган, маанилердин къпт\г\ аталат. Мисалы: барабарсыздыгынын аныкталуу областы
барабарсыздыгынын аныкталуу областы  .
.
Барабарсыздыкка катышкан туюнтмаларга карап барабарсыздыктар тъмънк\дъй болуп бъл\нът: алгебралык, кърсътк\чт\\, логарифмдик, тригонометриялык жана тескери тригонометриялык.
Аныктама: Эгер барабрсыздыкка алгебралык туюнтмалар катышса, анда барабарсыздык алгебралык деп аталат.
Аныктама: Эгер  болсо, анда
болсо, анда 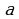 b дан кичине, ал эми
b дан кичине, ал эми  болсо, анда a b дан чоё деп аталат.
болсо, анда a b дан чоё деп аталат.
Аныктама: Ъзгърмълърд\н кабыл алууга м\мк\н болгон бардык маанилеринде туура болгон барабарсыздык теёдеш барабарсыздык деп аталат.
Мисалы:
Барабарсыздыктардын касиеттери.
Барабарсыздыктардын негизги касиеттери тъмънк\лър:
Эгер 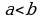 болсо,анда
болсо,анда 
Эгер 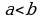 жана
жана 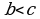 болсо,анда
болсо,анда 
Эгер 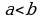 жана
жана 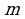 - каалаган сан болсо, анда
- каалаган сан болсо, анда 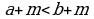
Эгер 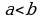 жана
жана  болсо, анда
болсо, анда 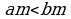 .
.
Натыйжа: Эгер 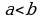 жана
жана 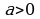 болсо, анда
болсо, анда 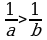 .
.
Эгер 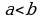 жана
жана 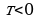 болсо, анда
болсо, анда 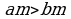 .
.
Эгер 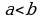 жана
жана 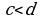 болсо, анда
болсо, анда 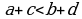 .
.
Эгер 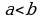 жана
жана 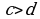 болсо, анда
болсо, анда  .
.
Эгер 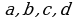 –оё сандар жана
–оё сандар жана  болсо, анда
болсо, анда 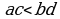 .
.
Эгер 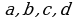 –оё сандар жана
–оё сандар жана 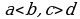 болсо, анда
болсо, анда  .
.
Эгер 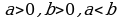 жана
жана 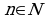 болсо, анда
болсо, анда  .
.
Эгер  жана
жана 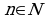 болсо, анда
болсо, анда 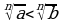 .
.
Бул касиеттердин айрымдарынын далилдеништерин келтирели, ал эми калгандары ъз алдынча далилдъъгъ сунуш кылынат.
2- касиетти далилдейли: Шарт боюнча  жана
жана  ал эми алардын суммасы дагы
ал эми алардын суммасы дагы 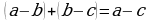 терс сан, ошондуктан
терс сан, ошондуктан  .
.
8-касиетти далилдейли: 4-касиет боюнча { 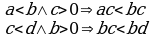 мында 2-касиет боюнча
мында 2-касиет боюнча 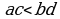
3. Барабарсыздыктарды далилдъъ жолдору.
Барабарсыздыктардын теёдештигин далилдъън\н тъмънк\дъй жолдору бар.
Эки сандын барабарсыздыгынын аныктамасына негиздъъ жолу.
Аналитикалык жолу, б.а. барабарсыздыктардын 1-11-касиеттерин колдонуу жолу менен далилдъъ.
Синтетикалык жолу, кайсы бир белгил\\ барабарсыздыктан пайдаланып берилген барабарсыздыкты далилдъъ.
Математикалык индукция методу.
Мурда далилденген барабарсыздыктан пайдалануу менен берилген барабарсыздыкты далилдъъ жолу.
Алгебралык белгил\\ барабарсыздыктардын айрымдарынан далилдъълър\н келтиребиз.
1.  , мында
, мында 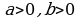 б.а. эки сандын арифметикалык орточосу менен геомет-риялык орточосунун арасындагы байланышты кърсът\\ч\ барабарсыздык. Бул барабар-сыздыкты далилдъън\н бир нече жолу бар.
б.а. эки сандын арифметикалык орточосу менен геомет-риялык орточосунун арасындагы байланышты кърсът\\ч\ барабарсыздык. Бул барабар-сыздыкты далилдъън\н бир нече жолу бар.
1). Эки сандын айырмасы боюнча далилдъъ:
 мында
мында экендиги келип чыгат.
экендиги келип чыгат.
2). Аналитикалык жол менен далилдъъ:  . Эки жагын 2ге къбъйт\п тъмън-к\н\ алабыз: 2
. Эки жагын 2ге къбъйт\п тъмън-к\н\ алабыз: 2 =
= а+в
а+в  2
2 . Барабарсыздыктын бардык м\чълър\н анын сол жагына алып ътъб\з.
. Барабарсыздыктын бардык м\чълър\н анын сол жагына алып ътъб\з. 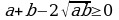 же (
же ( -
- 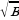 )2
)2  0 экендигин алууга болот, ал эми бул барабрсыздык
0 экендигин алууга болот, ал эми бул барабрсыздык 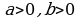 болгон учурда ар дайым туура.
болгон учурда ар дайым туура.
3). Синтетикалык жол менен далилдъъ: (а-в)2 0 барабарсыздыгы ар дайым туура экендиги белгил\\
0 барабарсыздыгы ар дайым туура экендиги белгил\\  . Барабарсыздыктын эки жагына теё 4 ab ны кошо-буз
. Барабарсыздыктын эки жагына теё 4 ab ны кошо-буз 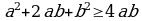 , андан
, андан  экендиги алынат. Мындан эки жагынан квадраттык тамыр чыгарабыз:
экендиги алынат. Мындан эки жагынан квадраттык тамыр чыгарабыз:  же
же  . Бул барабарсыздык
. Бул барабарсыздык 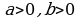 шарты \ч\н туура.
шарты \ч\н туура.
2. Эгер а 0, в
0, в 0, с
0, с 0 жана
0 жана 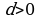 болсо, анда
болсо, анда 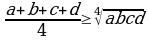
3. Эгер 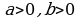 жана
жана 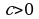 болсо, анда
болсо, анда 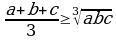
4. Кошинин барабарсыздыгы:  . n оё сандан арифиметикалык орточосу менен геометриялык орточосунун арасындагы байланышты кърсът\\ч\ барабар-сыздык.
. n оё сандан арифиметикалык орточосу менен геометриялык орточосунун арасындагы байланышты кърсът\\ч\ барабар-сыздык.
 арифиметикалык орточо менен квадраттык орточонун байланышы.
арифиметикалык орточо менен квадраттык орточонун байланышы.
 гармоникалык орточо менен геометриялык орточонун байланышы.
гармоникалык орточо менен геометриялык орточонун байланышы.
Кошинин барабарсыздыгы: 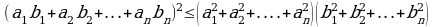
Бернулли барабарсыздыгы: каалаган a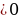 , r
, r 0 \ч\н
0 \ч\н  r- рационалдык сан.
r- рационалдык сан.
9. Эгер  болсо, анда
болсо, анда  ъз ара тескери сандардын суммасы жън\ндъг\ барабарсыздык
ъз ара тескери сандардын суммасы жън\ндъг\ барабарсыздык
Каалаган 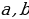 , c сандары
, c сандары 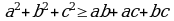 .
.
Далилдъъ: 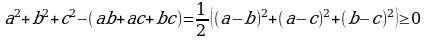
болгондуктан 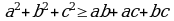 .
.
Бернулинин барабарсыздыгын далилдейли: Айталы 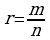 , болсо, мында m,n –натуралдык сандар жана
, болсо, мында m,n –натуралдык сандар жана 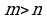 . Кошинин барабарсыздыгы боюнча
. Кошинин барабарсыздыгы боюнча
 же
же 
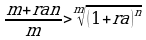 же
же  .
.  болгондуктан
болгондуктан 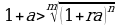
Бул барабарсыздыкты m -даражага кътъръб\з:  мындан n - даражалуу тамыр чыгарып
мындан n - даражалуу тамыр чыгарып 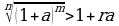 же
же 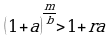 ны алабыз.
ны алабыз. 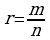 менен алмаштырып тъмънк\н\ алабыз:
менен алмаштырып тъмънк\н\ алабыз: 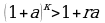
Кън\г\\лър.
а нын каалаган маанисинде барабарсзыдык туура экендигин далилдегиле.
 .
.



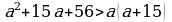
 .
.

 , мында
, мында  .
.
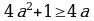

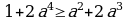
 мында
мында 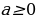 ,
, 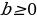
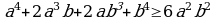 мында a,b- бирдей белгидеги сандар.
мында a,b- бирдей белгидеги сандар.
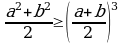 , мында
, мында 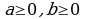 .
.
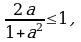 мында
мында 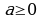 .
.
 , мында
, мында 
 , мында
, мында 

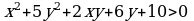



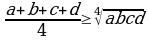 мында
мында  ,
,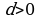
 , мында
, мында 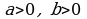
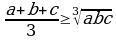 , мында
, мында 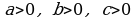
 мында
мында  ,
,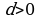
Эгерде  болсо, анда
болсо, анда 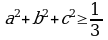

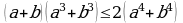
 мында
мында 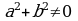
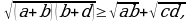 мында
мында 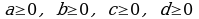
Эгер  болсо, анда
болсо, анда 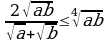
Эгер 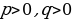 болсо, анда
болсо, анда 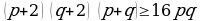
Эгер 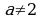 болсо, анда
болсо, анда 
Эгер m, n, p -\ч бурчтуктун жактарынын узундуктары болсо, анда 
Эгер 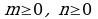 болсо, анда
болсо, анда 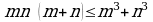
 .
.

 мында
мында 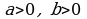
 мында
мында 
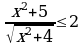 , мында
, мында 
 .
.
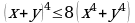 .
.

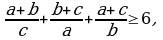 мында
мында 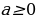 ,
, 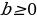 ,
, 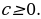
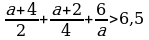 мында
мында 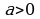
 мында
мында 
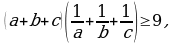 мында
мында 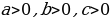 .
.
 мында
мында 
 мында
мында  ,
,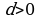
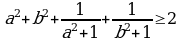
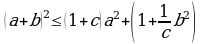 , мында
, мында 

 мында
мында 








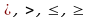 белгилери аркылуу бириктирилип жазылышы барабарсыздык деп аталат.
белгилери аркылуу бириктирилип жазылышы барабарсыздык деп аталат. ж.б.
ж.б. белгиси аркылуу бириктирилип жазылы-шын айтууга болот. Мисалы:
белгиси аркылуу бириктирилип жазылы-шын айтууга болот. Мисалы: 
 барабарсыздыгынын аныкталуу областы
барабарсыздыгынын аныкталуу областы  .
. болсо, анда
болсо, анда 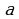 b дан кичине, ал эми
b дан кичине, ал эми  болсо, анда a b дан чоё деп аталат.
болсо, анда a b дан чоё деп аталат.
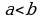 болсо,анда
болсо,анда 
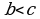 болсо,анда
болсо,анда 
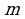 - каалаган сан болсо, анда
- каалаган сан болсо, анда 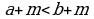
 болсо, анда
болсо, анда 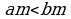 .
. 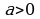 болсо, анда
болсо, анда 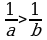 .
.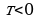 болсо, анда
болсо, анда 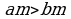 .
.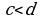 болсо, анда
болсо, анда 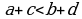 .
.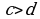 болсо, анда
болсо, анда  .
.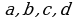 –оё сандар жана
–оё сандар жана  болсо, анда
болсо, анда 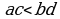 .
.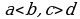 болсо, анда
болсо, анда  .
.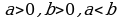 жана
жана 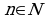 болсо, анда
болсо, анда  .
. жана
жана 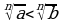 .
. ал эми алардын суммасы дагы
ал эми алардын суммасы дагы 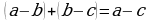 терс сан, ошондуктан
терс сан, ошондуктан 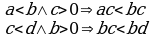 мында 2-касиет боюнча
мында 2-касиет боюнча  , мында
, мында 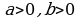 б.а. эки сандын арифметикалык орточосу менен геомет-риялык орточосунун арасындагы байланышты кърсът\\ч\ барабарсыздык. Бул барабар-сыздыкты далилдъън\н бир нече жолу бар.
б.а. эки сандын арифметикалык орточосу менен геомет-риялык орточосунун арасындагы байланышты кърсът\\ч\ барабарсыздык. Бул барабар-сыздыкты далилдъън\н бир нече жолу бар. мында
мында экендиги келип чыгат.
экендиги келип чыгат. =
= а+в
а+в  2
2 . Барабарсыздыктын бардык м\чълър\н анын сол жагына алып ътъб\з.
. Барабарсыздыктын бардык м\чълър\н анын сол жагына алып ътъб\з. 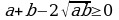 же (
же ( -
- 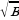 )2
)2  . Барабарсыздыктын эки жагына теё 4 ab ны кошо-буз
. Барабарсыздыктын эки жагына теё 4 ab ны кошо-буз 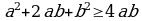 , андан
, андан  экендиги алынат. Мындан эки жагынан квадраттык тамыр чыгарабыз:
экендиги алынат. Мындан эки жагынан квадраттык тамыр чыгарабыз:  же
же 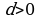 болсо, анда
болсо, анда 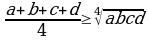
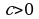 болсо, анда
болсо, анда 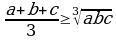
 . n оё сандан арифиметикалык орточосу менен геометриялык орточосунун арасындагы байланышты кърсът\\ч\ барабар-сыздык.
. n оё сандан арифиметикалык орточосу менен геометриялык орточосунун арасындагы байланышты кърсът\\ч\ барабар-сыздык. арифиметикалык орточо менен квадраттык орточонун байланышы.
арифиметикалык орточо менен квадраттык орточонун байланышы. гармоникалык орточо менен геометриялык орточонун байланышы.
гармоникалык орточо менен геометриялык орточонун байланышы.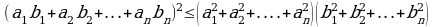
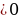 , r
, r r- рационалдык сан.
r- рационалдык сан. болсо, анда
болсо, анда  ъз ара тескери сандардын суммасы жън\ндъг\ барабарсыздык
ъз ара тескери сандардын суммасы жън\ндъг\ барабарсыздык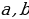 , c сандары
, c сандары 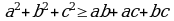 .
.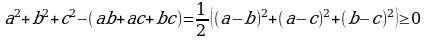
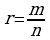 , болсо, мында m,n –натуралдык сандар жана
, болсо, мында m,n –натуралдык сандар жана 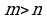 . Кошинин барабарсыздыгы боюнча
. Кошинин барабарсыздыгы боюнча же
же 
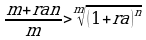 же
же  .
.  болгондуктан
болгондуктан 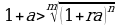
 мындан n - даражалуу тамыр чыгарып
мындан n - даражалуу тамыр чыгарып 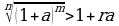 же
же 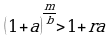 ны алабыз.
ны алабыз. 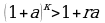
 .
. 


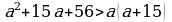
 .
.
 , мында
, мында  .
.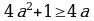

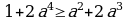
 мында
мында 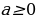 ,
, 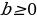
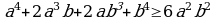 мында a,b- бирдей белгидеги сандар.
мында a,b- бирдей белгидеги сандар.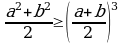 , мында
, мында 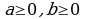 .
.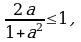 мында
мында 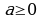 .
. , мында
, мында 
 , мында
, мында 

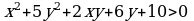



 ,
, , мында
, мында 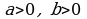
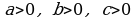
 мында
мында  ,
, болсо, анда
болсо, анда 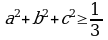

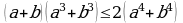
 мында
мында 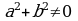
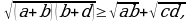 мында
мында 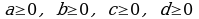
 болсо, анда
болсо, анда 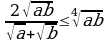
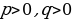 болсо, анда
болсо, анда 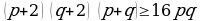
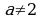 болсо, анда
болсо, анда 

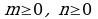 болсо, анда
болсо, анда 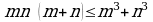
 .
.
 мында
мында 
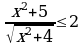 , мында
, мында  .
. 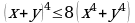 .
.
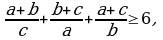 мында
мында 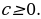
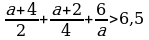 мында
мында  мында
мында 
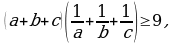 мында
мында 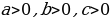 .
. мында
мында  мында
мында 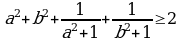
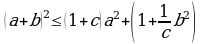 , мында
, мында 

 мында
мында 

















